| Меню сайта |
| | |
 |
| Категории раздела |
| | |
 |
| Вход на сайт |
| | |
 |
| Поиск |
| | |
 |
| Календарь |
|
| « Май 2017 » |
| Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | | 8 | 9 | 10 | 11 | 12 | 13 | 14 | | 15 | 16 | 17 | 18 | 19 | 20 | 21 | | 22 | 23 | 24 | 25 | 26 | 27 | 28 | | 29 | 30 | 31 | | |
 |
| Архив записей |
| | |
 |
| Статистика |
|
Онлайн всего: 1 Гостей: 1 Пользователей: 0 | |
 |
|
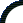 | |  |
| Главная » 2017 » Май » 26 » Пневмогидравлическая ракета
13:03 Пневмогидравлическая ракета |
[править | править вики-текст]
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Старт пневмогидравлической ракеты, кустарно изготовленной из ПЭТ-бутылок
Пневмогидравлическая ракета, водяная ракета — ракета, использующая в качестве рабочего тела воду (или другую жидкость), вытесняемую из корпуса ракеты через сопло давлением сжатого воздуха или иного газа. Получили распространение, в основном, в качестве игрушек. Используются также для демонстрации принципов реактивного движения.
Динамика пневмогидравлической ракеты[править | править вики-текст]
Схема пневмогидравлической ракеты
Сжатый воздух при истечение из сопла ракеты способен создавать тягу без жидкости-посредника. Однако масса воздуха в корпусе ракеты ограничена. Более выгодным представляется использование в качестве рабочего тела жидкости. В виду того, что через сопло пневмогидравлической ракеты истекает жидкость, оно выполняется не в форме сопла Лаваля, а имеет плавно очерченную сужающуюся форму.
Максимальную скорость истечения жидкости из сопла пневмогидравлической ракеты можно определить исходя из закона Бернулли:
ρ
v
2
2
=
Δ
p
{\displaystyle {\frac {\rho v^{2}}{2}}=\Delta p}
,
где
ρ
{\displaystyle \rho }
- плотность жидкости;
v
{\displaystyle v}
- скорость истечения жидкости;
Δ
p
{\displaystyle \Delta p}
- избыточное давление газа в ракете.
Сопло пневмогидравлической ракеты чаще всего представляет собой сужающийся профилированный насадок с малым отрывом струи. Фактический объемный расход жидкости через сопло составит:
Q
=
μ
S
0
2
Δ
p
ρ
{\displaystyle Q=\mu S_{0}{\sqrt {\frac {2\Delta p}{\rho }}}}
μ
=
0
,
6..0
,
8
{\displaystyle \mu =0,6..0,8}
- коэффициент расхода
S
0
{\displaystyle S_{0}}
- площадь узкой части сопла
Массовый расход жидкости составит:
G
=
Q
ρ
=
μ
S
0
2
ρ
Δ
p
{\displaystyle G=Q\rho =\mu S_{0}{\sqrt {2\rho \Delta p}}}
Сила тяги составит:
F
=
Q
v
=
2
μ
S
0
Δ
p
{\displaystyle F=Qv=2\mu S_{0}\Delta p}
Время действия пневмогидравлического двигателя, при условии что жидкость будет израсходована раньше, чем сжатый газ составит:
T
=
m
G
{\displaystyle T={\frac {m}{G}}}
m
{\displaystyle m}
- масса жидкости на старте ракеты
Литература[править | править вики-текст]
Беляев Н. М. Расчет пневмогидравлических систем ракет : [рус.] : учебное пособие. — М. : Машиностроение, 1983. — 219 с.
Ссылки[править | править вики-текст]
Подробный расчет пневногидравлической ракеты (англ.)
Это заготовка статьи об игрушке. Вы можете помочь проекту, дополнив её.
Возможно, эта статья содержит оригинальное исследование.
Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление.
Дополнительные сведения могут быть на странице обсуждения. (8 июля 2014)
Для улучшения этой статьи желательно:
Проверить достоверность указанной в статье информации.

Источник — «https://ru.wikipedia.org/w/index.php?title=Пневмогидравлическая_ракета&oldid=85103688»
Категории: РакетыЛетающие игрушкиГидравликаИгрушки, демонстрирующие физические законыСкрытые категории: Незавершённые статьи об игрушкахВикипедия:Статьи, подозреваемые в наличии оригинальных исследований с июля 2014 годаВикипедия:Статьи, достоверность которых требует проверки
|
|
Категория: Необычное |
Просмотров: 123 |
Добавил: alena_soboleva_70
| Рейтинг: 0.0/0 |
| |
 | |  |
|






